Henri Poincaré war ein französischer Mathematiker des 19. und 20. Jahrhunderts. Er gilt als Begründer der algebraischen Topologie und beschäftigte sich auch mit der Zahlentheorie, theoretischen Physik und Philosophie. Anlässlich seines 158. Geburtstags werfen wir heute einen Blick auf sein Leben und Wirken. Er war einer der letzten Mathematiker, der sowohl die reine als auch die angewandte Mathematik komplett überblickte. Seine Bücher wie „Science and Method“ (1914), die allgemeinverständlich über die Grundlagen der Wissenschaft aufklärten, hatten eine nachhaltige Wirkung und trugen zum Interesse an den Problemen der modernen Mathematik bei.
Kindheit in Nancy
Am 29. April 1854, also vor 158 Jahren, wurde Jules Henri Poincaré in Nancy geboren. Seine Familie war gebildet und einflussreich, sein Cousin Raymond Poincaré wurde sogar Minister- und Staatspräsident Frankreichs. Henri Poincaré wurde aufgrund seiner Diphterie-Erkrankung einige Jahre von seiner Mutter zu Hause unterrichtet. Anschließend besuchter er das Lyzeum in Nancy.
Studium in Paris
Ab 1873 studierte Henri Poincaré Mathematik an der Eliteuniversität École polytechnique in Paris. Ein Jahr später folgte seine erste Veröffentlichung. Er wechselte an die École des Mines, wo er 1879 seinen Abschluss als Bergbau-Ingenieur machte. Auch wenn Poincaré später als Mathematiker arbeitet und berühmt wurde, gab er seine Tätigkeiten als Ingenieur nie komplett auf. Als Doktorand von Charles Hermite erhielt Poincaré 1879 seinen Doktortitel.
Beruflicher Werdegang
Ab 1879 hielt er Vorlesungen zur Mathematik und Physik an verschiedenen Universitäten in Frankreich. Henri Poincaré unterrichtete erst an der Universität Caen und anschließend in Paris. Er hatte mehrere Lehrstühle zur Mathematik und theoretischen Physik inne, die er Zeit seines Lebens behielt. Von 1881 bis 1885 arbeitete er für ein französisches Ministerium und setzte seine Tätigkeiten als Mineningenieur fort. 1893 trat er in das französische Bureau des Longitudes ein, dass für die Synchronisation der Weltzeit verantwortlich war.
Poincaré-Vermutung
Bei der Poincaré-Vermutung geht es nun um Flächen und vor allem darum, wie viele Löcher eine geschlossene Fläche hat. Eine Kugel beispielsweise, wir können sie uns als Ballon oder Ball vorstellen, ist eine geschlossene Fläche ohne Loch. Mathematisch nennt man diese Form Sphäre (Kugeloberfläche). Einen Ballon kann ich nun drücken, knoten und biegen – letztendlich behält man aber eine zusammenhängende Fläche ohne Loch.
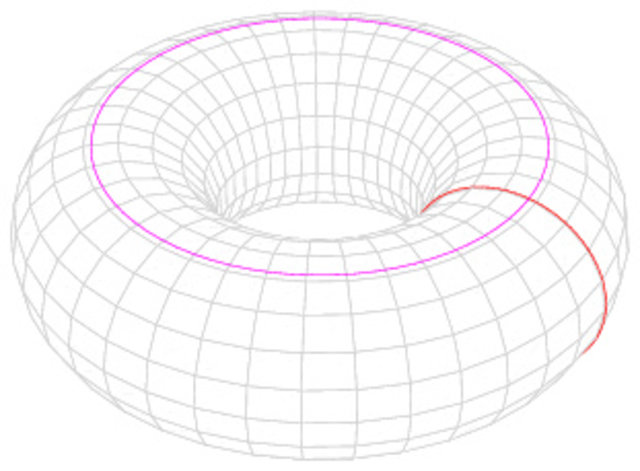
Ein Donut (bzw. seine Oberfläche) ist ebenfalls eine zusammenhängende Fläche. Allerdings hat sie ein Loch in der Mitte. Diese Form kann ich nun auch biegen und drücken, aber ich kann sie nie in eine Sphäre verformen.
Die Poincaré-Vermutung besagt nun, dass jede Form, die kein Loch hat, zu einer Kugel deformiert werden kann, zum Beispiel durch drücken oder ähnliches. Außerdem gilt diese Regel nicht nur für zweidimensionale Flächen in unserem dreidimensionalen Raum, sondern auch in höheren Dimensionen. Besonders im Falle der dreidimensionalen Oberfläche im vierdimensionalen Raum kann diese Aussage neue Erkenntnisse über die Geometrie des Universums ermöglichen.
Poincaré erklärt die topologische Analogie einer Fläche zur Sphäre anhand von Gummibändern, die man auf einen Punkt zusammenziehen kann, wenn die Fläche keine Löcher hat. Dies muss für alle Bänder gelten, die man um die Fläche spannen kann
Im Gegensatz zur Sphäre kann man beim Torus Gummibänder finden, die man nicht auf einen Punkt zusammenziehen kann. Sphäre und Torus sind topologisch also nicht gleich (nicht homöomorph).
Die Poincaré-Vermutung galt lange als eines der bedeutendsten ungelösten Probleme in der Topologie. Henri Poincaré hat sie bereits 1904 aufgestellt. Im Jahr 2000 zählte das Clay Mathematics Institute die Poincaré-Vermutung zu den sieben bedeutendsten ungelösten mathematischen Problemen, den Millennium-Problemen, und lobte für ihre Lösung eine Million US-Dollar aus. Grigori Perelman hat die Vermutung bewiesen. 2006 sollte er die Fields-Medaille für seinen Beweis erhalten, die er jedoch ablehnte. Am 18. März 2010 wurde ihm außerdem der Millennium-Preis des Clay Mathematics Institut zugesprochen, den er ebenfalls ablehnte.
Intuition als Merkmal seiner Arbeit
Poincarés Arbeiten waren stets von seiner intuitiven Art und Originalität geprägt. Viele seiner Veröffentlichungen waren auch für Nicht-Wissenschaftler verständlich und philosophisch, beispielsweise sein Artikel „The Relativity of Space“, der 1897 in „Science and Method“ erschienen ist.
Er gilt als der Begründer der algebraischen Topologie, dem Gebiet der Mathematik, das sich mit der Funktionentheorie mehrerer komplexer Variablen beschäftigt. Außerdem beschäftigte er sich mit Differentialgleichungen, algebraischer Geometrie und nicht-euklidischer Geometrie. Im Bereich der Zahlentheorie brachte Poincaré viele Arbeiten und Beweise zu den diophantischen Gleichungen hervor.
Auch zu Themen der Physik veröffentlichte Poincaré regelmäßig. So verfasste er Arbeiten zu Elektrizität, Optik, Thermodynamik und später auch zur Quantentheorie. Insbesondere beschäftigte er sich mit dem 3-Körper-Problem.
Neben diesen hochwissenschaftlichen Arbeiten verfasste er einige populärwissenschaftliche Werke wie „Science and Method“ oder „The Value of Science“. Sein Bestreben, die Zusammenhänge der Welt vor allem verständlich zu erklären, hat wohl dazu beigetragen, dass man ihn als letzten Universalist in der Mathematik wahrgenommen hat.
Henri Poincaré brachte es Zeit seines Lebens auf knapp 250 Publikationen zur Topologie, komplexe Funktionen, Differentialgleichungen, Wahrscheinlichkeitstheorie, Zahlentheorie, Optik, Himmelsmechanik und vielem mehr. Er starb am 17. Juli 1912 in Paris.
Zum Weiterlesen:
- Bibliographie und Korrespondenzen von der Universität Nancy
- Poincarés philosophischer Artikel „The Relativity of Space“ aus der Zeitschrift Science & Method, erschienen 1897 (englisch)
- verschiedene Ingenieurs-Arbeiten Poincarés mit vielen Bildern von Pierre Driout (englisch, französisch)
- Radiopodcast der BBC, moderiert von Marcus du Sautoy über die Geschichte der Mathematiker, Teil 8: Henri Poincaré
- Eintrag zu Henri Poincaré in der Encyclopaedia Britannica, mit vielen weiterführenden Verlinkungen
- Biografie mit vielen Zitaten und Glossar der Universität St. Andrews